All distances within a selection

Here we calculate the distance of every atom to every other atom in a selection, and show how we can extend this to residues.

Last updated: December 2022 with MDAnalysis 2.4.0-dev0

Minimum version of MDAnalysis: 0.19.0

Packages required:

• MDAnalysis ([MADWB11], [GLB+16])

• MDAnalysisTests

Optional packages for visualisation:

• matplotlib

import MDAnalysis as mda
from MDAnalysis.tests.datafiles import PDB_small
from MDAnalysis.analysis import distances

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

import warnings
# suppress some MDAnalysis warnings when writing PDB files
warnings.filterwarnings('ignore')

Loading files

The test files we will be working with here feature adenylate kinase (AdK), a phosophotransferase enzyme. ([BDPW09])

u = mda.Universe(PDB_small)

Calculating atom-wise distances

We begin by selecting the alpha-carbons of the protein.

ca = u.select_atoms('name CA')
n_ca = len(ca)
n_ca

214

When given an array with \(n\) positions, distances.self_distance_array (API docs) returns the distances in a flat vector with length \(\frac{n(n-1)}{2}\). These correspond to the flattened upper triangular values of a square distance matrix.

self_distances = distances.self_distance_array(ca.positions)
self_distances.shape

(22791,)

We can convert this into a more easily interpreted square distance array. First we create an all-zero square array and get the indices of the upper and lower triangular matrices.

sq_dist_arr = np.zeros((n_ca, n_ca))
triu = np.triu_indices_from(sq_dist_arr, k=1)

Then we simply assign the calculated distances to the upper and lower triangular positions.

sq_dist_arr[triu] = self_distances
sq_dist_arr.T[triu] = self_distances

Plotting

fig, ax = plt.subplots()
im = ax.pcolor(ca.resids, ca.resids, sq_dist_arr)

# plt.pcolor gives a rectangular grid by default
# so we need to make our heatmap square
ax.set_aspect('equal')

# add figure labels and titles
plt.ylabel('Residue IDs')
plt.xlabel('Residue IDs')
plt.title('Distance between alpha-carbons in AdK')

# colorbar
cbar = fig.colorbar(im)
cbar.ax.set_ylabel('Distance (Angstrom)')

Text(0, 0.5, 'Distance (Angstrom)')

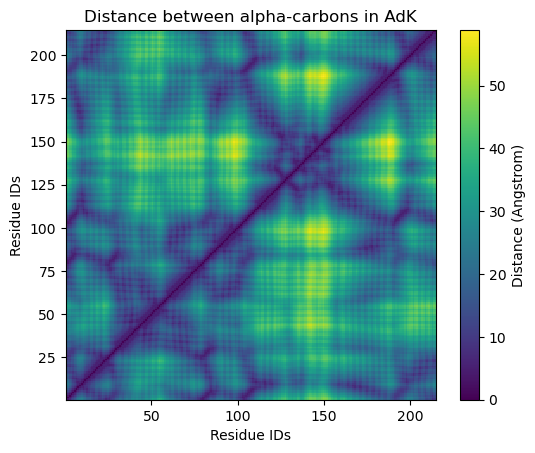
Calculating distances for each residue

Instead of calculating the distance between the alpha-carbon of each residue, we could look at the distances between the centers-of-mass instead. The process is very similar to the atom-wise distances above, but we have to pass distances.self_distance_array an array of residue center-of-mass coordinates instead.

res_com = u.atoms.center_of_mass(compound='residues')
n_res = len(res_com)
n_res

214

As the number of residues remains the same, the resulting distances array has the same length.

res_dist = distances.self_distance_array(res_com)
res_dist.shape

(22791,)

This means we don’t need to re-define triu.

sq_dist_res = np.zeros((n_res, n_res))
sq_dist_res[triu] = res_dist
sq_dist_res.T[triu] = res_dist

Plotting

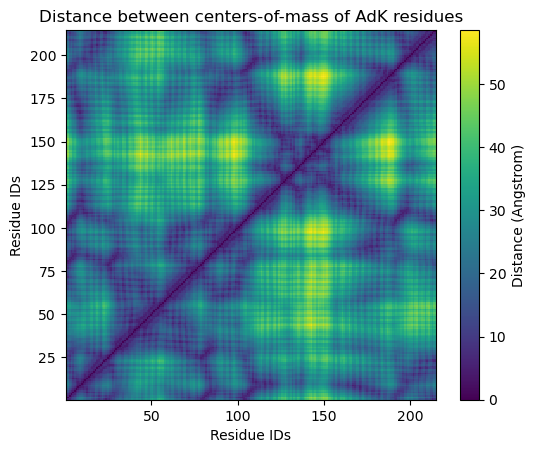
The resulting plot looks pretty similar.

fig2, ax2 = plt.subplots()
im2 = ax2.pcolor(u.residues.resids, u.residues.resids, sq_dist_res)

# plt.pcolor gives a rectangular grid by default
# so we need to make our heatmap square
ax2.set_aspect('equal')

# add figure labels and titles
plt.ylabel('Residue IDs')
plt.xlabel('Residue IDs')
plt.title('Distance between centers-of-mass of AdK residues')

# colorbar
cbar2 = fig2.colorbar(im2)
cbar2.ax.set_ylabel('Distance (Angstrom)')

Text(0, 0.5, 'Distance (Angstrom)')

References

[1] Oliver Beckstein, Elizabeth J. Denning, Juan R. Perilla, and Thomas B. Woolf. Zipping and Unzipping of Adenylate Kinase: Atomistic Insights into the Ensemble of Open↔Closed Transitions. Journal of Molecular Biology, 394(1):160–176, November 2009. 00107. URL: https://linkinghub.elsevier.com/retrieve/pii/S0022283609011164, doi:10.1016/j.jmb.2009.09.009.

[2] Richard J. Gowers, Max Linke, Jonathan Barnoud, Tyler J. E. Reddy, Manuel N. Melo, Sean L. Seyler, Jan Domański, David L. Dotson, Sébastien Buchoux, Ian M. Kenney, and Oliver Beckstein. MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations. Proceedings of the 15th Python in Science Conference, pages 98–105, 2016. 00152. URL: https://conference.scipy.org/proceedings/scipy2016/oliver_beckstein.html, doi:10.25080/Majora-629e541a-00e.

[3] Naveen Michaud-Agrawal, Elizabeth J. Denning, Thomas B. Woolf, and Oliver Beckstein. MDAnalysis: A toolkit for the analysis of molecular dynamics simulations. Journal of Computational Chemistry, 32(10):2319–2327, July 2011. 00778. URL: http://doi.wiley.com/10.1002/jcc.21787, doi:10.1002/jcc.21787.