Helix analysis

We look at protein helices with HELANAL.

Last updated: December 2022 with MDAnalysis 2.4.0-dev0

Minimum version of MDAnalysis: 2.0.0

Packages required:

• MDAnalysis ([MADWB11], [GLB+16])

• MDAnalysisTests

Optional packages for visualisation:

• matplotlib

• nglview

Throughout this tutorial we will include cells for visualising Universes with the NGLView library. However, these will be commented out, and we will show the expected images generated instead of the interactive widgets.

Note

MDAnalysis.analysis.helix_analysis.HELANAL implements the HELANAL algorithm from [BKV00], which itself uses the method of [SM67] to characterise each local axis. Please cite them when using this module in published work.

import MDAnalysis as mda
from MDAnalysis.tests.datafiles import PSF, DCD
from MDAnalysis.analysis import helix_analysis as hel
import matplotlib.pyplot as plt
# import nglview as nv
%matplotlib inline

Loading files

The test files we will be working with here feature adenylate kinase (AdK), a phosophotransferase enzyme. ([BDPW09])

u = mda.Universe(PSF, DCD)

/Users/lily/pydev/mdanalysis/package/MDAnalysis/coordinates/DCD.py:165: DeprecationWarning: DCDReader currently makes independent timesteps by copying self.ts while other readers update self.ts inplace. This behavior will be changed in 3.0 to be the same as other readers. Read more at https://github.com/MDAnalysis/mdanalysis/issues/3889 to learn if this change in behavior might affect you.
  warnings.warn("DCDReader currently makes independent timesteps"

Helix analysis

HELANAL can be used to characterize the geometry of helices with at least 9 residues. The geometry of an alpha helix is characterized by computing local helix axes and local helix origins for four contiguous C-alpha atoms, using the procedure of Sugeta and Miyazawa ([SM67]) and sliding this window over the length of the helix in steps of one C-alpha atom.

HELANAL computes a number of properties.

For each sliding window, it calculates:

• local_rotation_vectors: the vectors bisecting the angles of the middle 2 atoms

• local_origins: the projected origins of the helix

• local_twists: the twist of each window (\(\theta\))

• residues_per_turn: how many residues would fit in a turn, based on local_twist

• local_axes: the axis of each local helix

• local_heights: the rise of each helix

HELANAL calculates the bends between each local_axes and fits the vector global_axes to the local_origins.

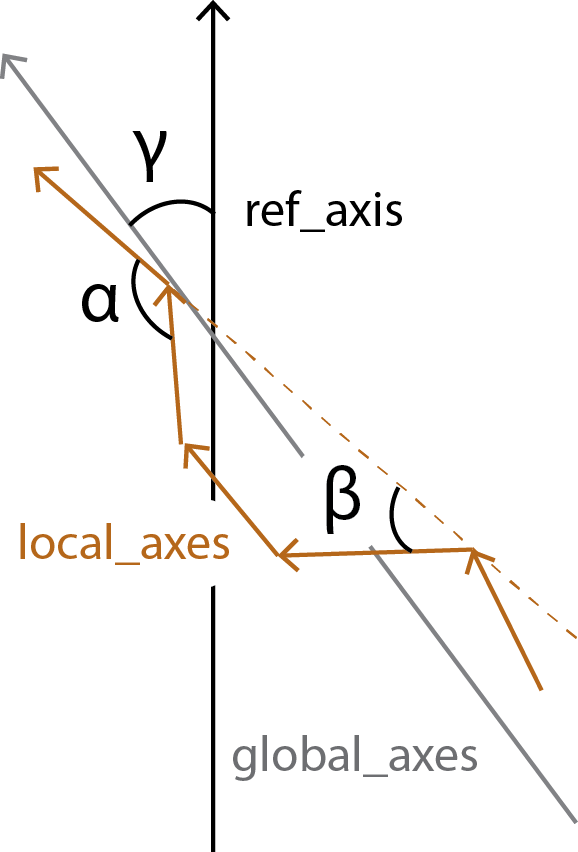
all_bends contains the angles between every local_axes (\(\alpha\)) in a pairwise matrix, whereas local_bends contains the angles between local_axes that are calculated 3 windows apart (\(\beta\)). The global_tilts (\(\gamma\)) are calculated as the angle between the global_axes and the user-given reference ref_axis.

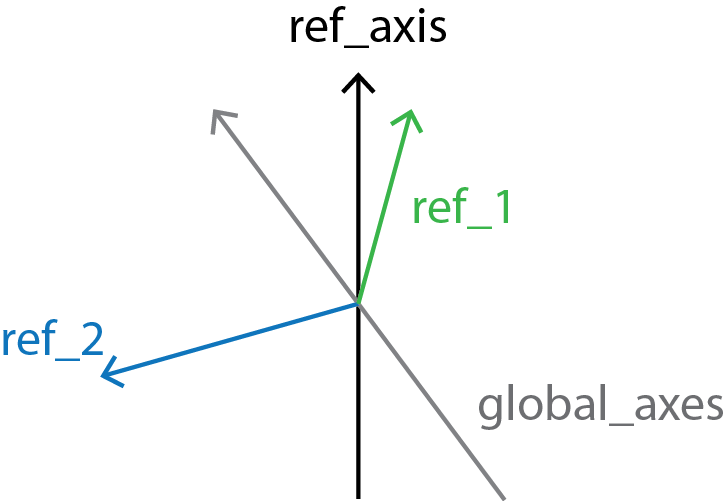
Finally, local_screw angles are computed between the local_rotation_vectors and the normal plane of the global_axes.

Running the analysis

As with most other analysis classes in MDAnalysis, pass in the universe and selection that you would to like to operate on. The default reference axis is the z-axis. You can also pass in a list of selection strings to run HELANAL on multiple helices at once.

h = hel.HELANAL(u, select='name CA and resnum 161-187',
                ref_axis=[0, 0, 1]).run()

The properties described above are stored as attributes in h.results. For example, the all_bends matrix contains the bends in a (n_frames, n_residues-3, n_residues-3) array.

h.results.all_bends.shape

(98, 24, 24)

Each property is also summarised with a mean value, the sample standard deviation, and the average deviation from the mean.

h.results.summary.keys()

dict_keys(['local_twists', 'local_bends', 'local_heights', 'local_nres_per_turn', 'local_origins', 'local_axes', 'local_helix_directions', 'local_screw_angles', 'global_axis', 'global_tilts', 'all_bends'])

for key, val in h.results.summary['global_tilts'].items():
    print(f"{key}: {val:.3f}")

mean: 86.121
sample_sd: 2.011
abs_dev: 1.715

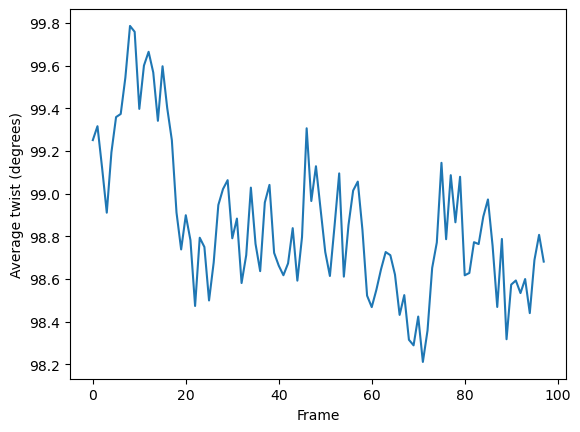
As the data is stored as arrays, it can easily be plotted.

plt.plot(h.results.local_twists.mean(axis=1))
plt.xlabel('Frame')
plt.ylabel('Average twist (degrees)')
plt.show()

You can also create a Universe from the local_origins if you would like to save it as a file and visualise it in programs such as VMD.

origins = h.universe_from_origins()

# view = nv.show_mdanalysis(h.atomgroups[0])
# view.add_trajectory(origins)
# view

Below we use NGLView to create a representative GIF.

# from nglview.contrib.movie import MovieMaker
# movie = MovieMaker(
#     view,
#     step=4,  # keep every 4th step
#     render_params={"factor": 3},  # controls quality
#     output='helanal_images/helanal-view.gif',
# )
# movie.make()

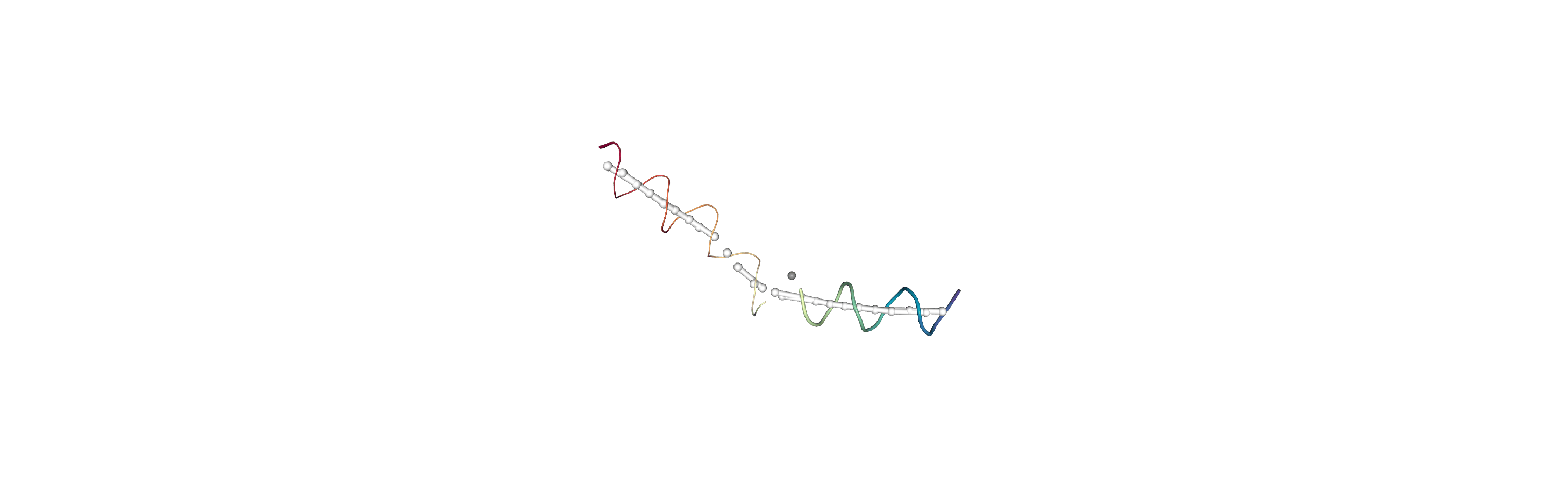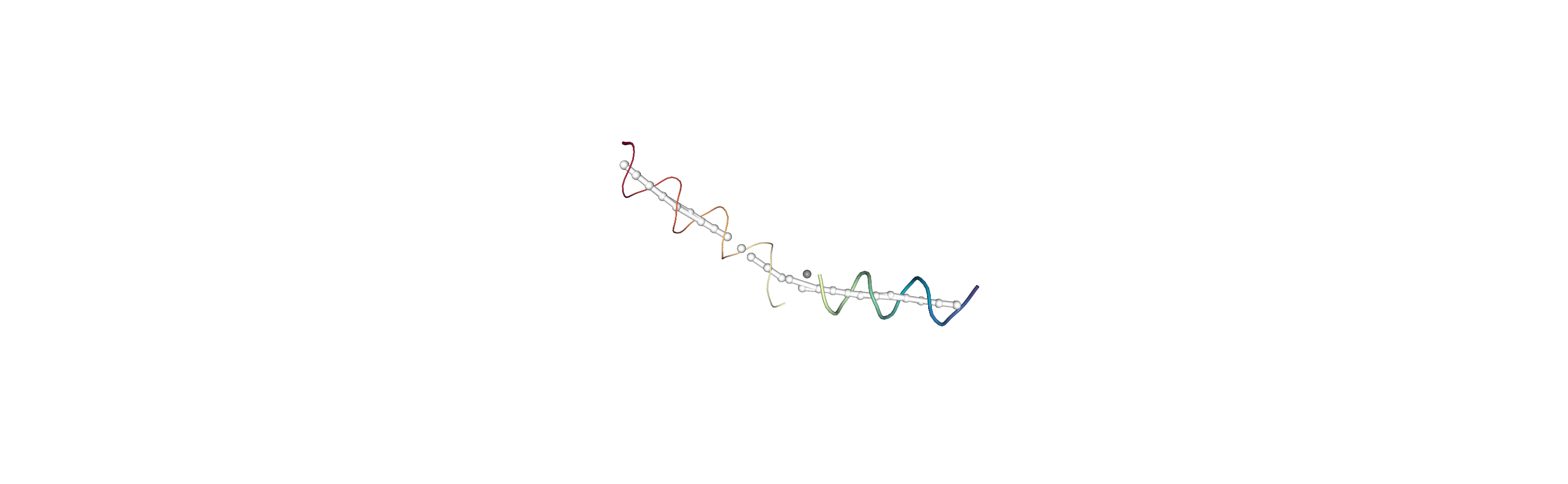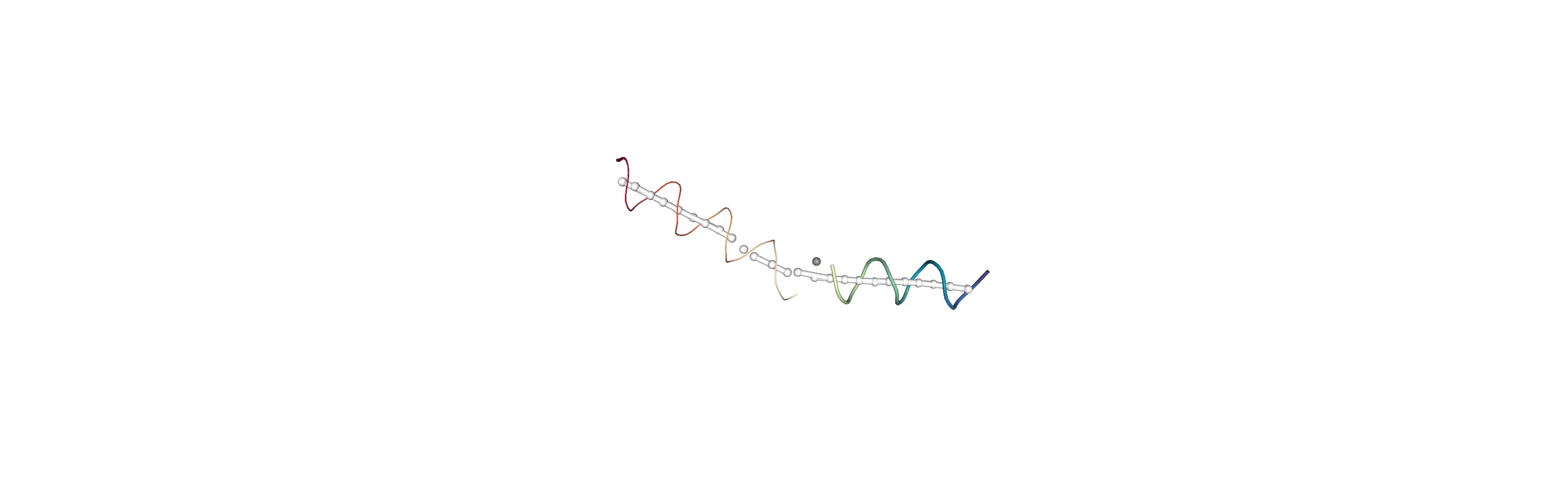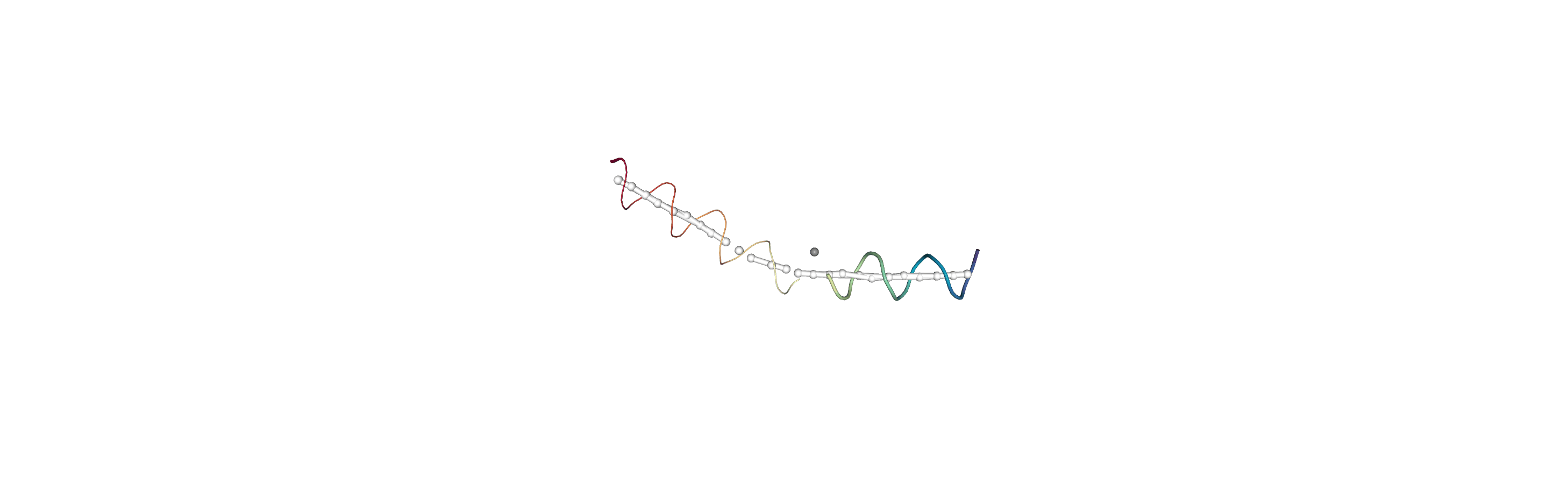
References

[1] M. Bansal, S. Kumar, and R. Velavan. HELANAL: a program to characterize helix geometry in proteins. Journal of Biomolecular Structure & Dynamics, 17(5):811–819, April 2000. 00175. doi:10.1080/07391102.2000.10506570.

[2] Oliver Beckstein, Elizabeth J. Denning, Juan R. Perilla, and Thomas B. Woolf. Zipping and Unzipping of Adenylate Kinase: Atomistic Insights into the Ensemble of Open↔Closed Transitions. Journal of Molecular Biology, 394(1):160–176, November 2009. 00107. URL: https://linkinghub.elsevier.com/retrieve/pii/S0022283609011164, doi:10.1016/j.jmb.2009.09.009.

[3] Richard J. Gowers, Max Linke, Jonathan Barnoud, Tyler J. E. Reddy, Manuel N. Melo, Sean L. Seyler, Jan Domański, David L. Dotson, Sébastien Buchoux, Ian M. Kenney, and Oliver Beckstein. MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations. Proceedings of the 15th Python in Science Conference, pages 98–105, 2016. 00152. URL: https://conference.scipy.org/proceedings/scipy2016/oliver_beckstein.html, doi:10.25080/Majora-629e541a-00e.

[4] Naveen Michaud-Agrawal, Elizabeth J. Denning, Thomas B. Woolf, and Oliver Beckstein. MDAnalysis: A toolkit for the analysis of molecular dynamics simulations. Journal of Computational Chemistry, 32(10):2319–2327, July 2011. 00778. URL: http://doi.wiley.com/10.1002/jcc.21787, doi:10.1002/jcc.21787.